2.2.2. Система індивідуалізованих завдань по темі
«Перетин поверхонь»

У нарисної геометрії розглядається два типи відносин між геометричними фігурами: позиційні і метричні. Вивчення теорії і алгоритмів вирішення позиційних і метричних задач в тривимірному розширеному евклідовому просторі направлено на розвиток «просторового мислення» студентів для подальшого читання і зіставлення креслень тривимірних об'єктів як на папері, так і на екрані монітора. Слід зауважити, що будь-яка форма деталі машини або механізму складається з дуг і відсіків абстрактних геометричних фігур (прямих і кривих ліній, площин, сфер, циліндрів, конусів і т.д.). Тому для їх конструювання, зображення, варіювання формою і розмірами необхідно вміти синтезувати їх з абстрактних геометричних тіл, будувати лінії перетину обмежують деталь поверхонь, визначати приналежність тих чи інших точок і ліній граней і поверхонь деталі.

В НГ позиційними завданнями прийнято називати такі, в яких потрібно визначити положення фігури щодо площин проекцій і взаємне положення (приналежність, паралельність, перетин) двох і більше фігур.

Положення фігури по відношенню до площин проекцій і зміна його для вирішення метричних задач розглядається в темі «Точка, пряма, площина і поверхня».

Навички визначення взаємного положення найпростіших геометричних фігур: точки і прямої, двох прямих, точки і площини, прямої і площини, двох площин формуються при вирішенні типових завдань на практичних заняттях. Розгляд позиційних задач з більш складними геометричними фігурами включено в індивідуальні графічні завдання.

Побудова лінії перетину поверхонь є найбільш цікавою і часто зустрічається в інженерній практиці позиційної завданням. Вона вирішується з використанням методу допоміжних січних поверхонь - посередників, правильний вибір яких визначає раціональність наступних геометричних побудов. Як поверхонь-посередників зазвичай використовують площині і сфери. При виборі посередників виходять з того, щоб вони перетинали досліджувані поверхні по графічно простим лініях - прямим і колах.

При вирішенні подібних завдань студент освоює такі обов'язкові вміння: вибору опорних точок, поверхні-посередника, знаходження проекцій точок лінії припинення та визначення її видимості. До умінням підвищеного рівня можна віднести перехід від плоского до наочному зображенню, побудова накладених перерізів проецирующей площиною, площиною загального положення, визначення їх натуральної величини.

Система завдань індивідуального графічного завдання по темі «Перетин поверхонь» представляють собою єдине ціле, елементи якого об'єднані ставленням приналежності до теми, і включає в себе 9 типів завдань:

1) циліндр з призматичним отвором;

2) конус з призматичним отвором;

3) куля з призматичним отвором;

4) перетин двох циліндрів;

5) перетин циліндра і конуса;

6) перетин циліндра і кулі;

7) перетин складовою поверхні і циліндра;

8) перетин складовою поверхні і конуса;

9) перетин складовою поверхні і кулі.

У завданнях 1, 2, 3 потрібно графічно визначити проекції точок лінії перетину поверхонь другого порядку з призмою; в задачах 4, 5, 6 - лінію перетину двох поверхонь другого порядку; в задачах 7, 8, 9 -лінію перетину поверхні другого порядку з складовою поверхнею, що включає відсік поверхні другого порядку і багатогранник. Очевидно, що запропонована система задовольняє вимогу передування менш складних завдань більш складним.

Всі типи завдань мають три рівні складності. Наприклад, в базовому рівні завдання «Конус з призматичним отвором» потрібно на підставі вихідних даних побудувати три проекції конуса з призматичним отвором і перетин в натуральну величину проецирующей площиною, заданої викладачем. Підвищення рівня складності відповідає додавання до базового рівня побудови розгортки поверхні конуса, високому - додаток перших двох побудов діметріческая зображенням. По кожному рівню є зразки оформлення рішення (див. Додаток 2 ).

Вихідні дані всіх завдань теми представлені з урахуванням рівня розвитку ПМ. Вони обов'язково включають в себе двовимірне зображення. Для того щоб врахувати відмінності в рівнях розвитку ПМ студентів кожне умова доповнено каркасної і тонованому моделями заданої фігури з можливістю перегляду зображення в графічному редакторі bCAD (рис.2). Звернення до гіперпосиланням свого варіанту дозволяє студенту побачити каркасну статичну модель фігури з можливістю переходу в режим тонованого перегляду і зміни точки відліку.

а)

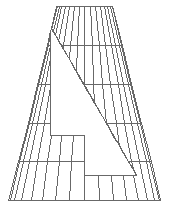
б)

в)

Малюнок 2. Умова задачі «Конус з призматичним отвором»

а) двовимірне зображення; б) каркасна модель; в) тонована модель

Завдання 1 - 6 також доповнюються словесним алгоритмом рішення, представленим в лекціях, який за бажанням студента може бути доповнений покрокової демонстрацією рішення на комп'ютері. У процесі перегляду рішення студент має можливість керувати швидкістю і напрямком зміни кадрів. Це дозволяє врахувати індивідуальну швидкість засвоєння навчального матеріалу студентом.

Наприклад, рішення базового рівня завдання «Перетин двох циліндрів» полягає в графічному знаходженні проекцій точок лінії перетину поверхонь на трьох проекціях по запропонованим вихідним даним: двовимірному зображенню і моделям (рис. 3). Підвищений рівень складності передбачає побудову перетину проецирующей площиною в натуральну величину, а високий - додаткове виконання накладених перерізів. Приклад покрокової демонстрації рішення базового рівня завдання, і зразки оформлення завдання відповідно до рівня наведено в додатку 3 .

а)

б)

в)

Малюнок 3. Умова завдання №4 «Перетин двох циліндрів»

а) двовимірне зображення; б) каркасна модель; в) тонована модель

Завдання 7 - 9 відносяться до евристичних, тому що алгоритм вирішення їх ніхто не знає студенту, а складається їм самостійно за допомогою розбиття вихідної задачі на підзадачі. Умови завдань представлені аналогічно попереднім - двовимірним зображенням (рис.4 а) і моделями (рис.4 б, в).

При вирішенні кожного завдання студенту надається можливість вибрати інструмент виконання рішення: традиційні креслярські інструменти або графічний редактор b CAD.

Використання графічного редактора дозволяє перевірити правильність результату порівнянням його з рішенням, виконаним автоматично відповідними інструментами bCAD (див. додаток 4 ).

Індивідуалізація завдань з інших тем проведена аналогічно.

а)

б)

в)

Малюнок 4. Умова завдання №7 «Перетин складовою поверхні і циліндра»

а) двовимірне зображення; б) каркасна модель; в) тонована модель