Наш бизнес-сообщник artMisto.net
Керівництво користувача Mathcad
Для вирішення одного рівняння з одним невідомим використовується функція root. Аргументами цієї функції є вираз і змінна, що входить у вираз. Шукається значення змінної, при якому вираз звертається в нуль. Функція повертає значення змінної, яке звертає вираз в нуль.
root(F (z), z) Повертає значення z, при якому вираз чи функція f (z) звертається до 0. Обидва аргументи цієї функції повинні бути скалярами.Функція повертає скаляр.
Перший аргумент є або функція, певна де-небудь в робочому документі, або вираз. Вираз повинен повертати скалярні значення.
Другий аргумент - ім'я змінної, яке використовується у виразі. Це та змінна, варіюючи яку Mathcad намагатиметься звернути вираз в нуль. Цієї змінної перед використанням функції root необхідно присвоїти числове значення. Mathcad використовує його як початкове наближення при пошуку кореня.
Розглянемо приклад, як знайти a - рішення рівняння ex = x3. Для цього виконайте наступні кроки:
- Визначте початкове значення змінної x. Введіть x: 3. Вибір початкового наближення впливає на корінь, що повертається Mathcad (якщо вираз має кілька коренів).
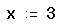
- Визначте вираз, яке повинно бути звернено в нуль. Для цього перепишіть рівняння ex = x3 у вигляді x3 - ex = 0. Ліва частина цього виразу і є другим аргументом функції root
- Визначте змінну a як корінь рівняння. Для цього введіть a: root (x ^ 3 [Space] -e ^ x [Space], x).
![Для цього введіть a: root (x ^ 3 [Space] -e ^ x [Space], x)](/wp-content/uploads/2020/01/uk-kerivnictvo-koristuvaca-mathcad-4.gif)
- Надрукуйте a =, щоб побачити значення кореня.
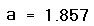
При використанні функції root майте на увазі наступне:
- Переконайтеся, що змінної присвоєно початкове значення до початку використання функції root.
- Для вираження з декількома країнами, наприклад x2 - 1 = 0, початкове значення визначає корінь, який буде знайдений Mathcad. На рисунку 1 наведено приклад, в якому функція root повертає різні значення, кожне з яких залежить від початкового наближення.
- Mathcad дозволяє знаходити як комплексні, так і речові коріння. Для пошуку комплексного кореня слід взяти в якості початкового наближення комплексне число.
- Завдання рішення рівняння виду f (x) = g (x) еквівалентна задачі пошуку кореня виразу f (x) - g (x) = 0. Для цього функція root може бути використана в такий спосіб:
root (f (x) - g (x), x)
Функція root призначена для вирішення одного рівняння з одним невідомим. Для вирішення систем рівнянь використовуйте методику, описану в наступному розділі "Системи рівнянь". Для символьного рішення рівнянь або знаходження точного чисельного рішення рівняння в термінах елементарних функцій виберіть Вирішити щодо змінної з меню Символіка. Див. Главу " Символьні обчислення ".
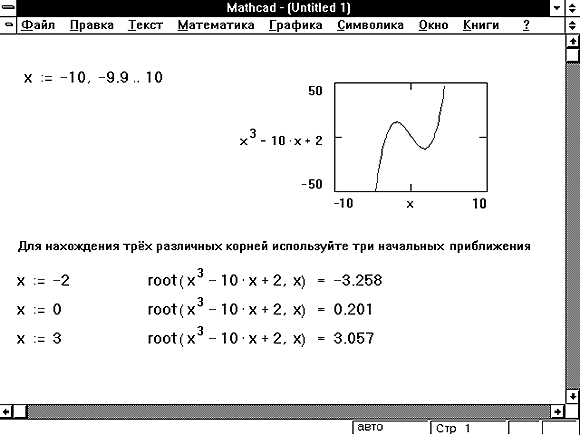
Малюнок 1: Використання графіка і функції root для пошуку коренів рівняння.
Що робити, коли функція root не сходиться
Mathcad в функції root іспользуетдля пошуку кореня метод січної. Початкове значення, присвоєне змінної x, стає першим наближенням до шуканого кореня. Коли значення виразу f (x) при черговому наближенні стає менше значення вбудованої змінної TOL, корінь вважається знайденим, і функція root повертає результат.
Якщо після багатьох ітерацій Mathcad не може знайти відповідного наближення, то з'являється повідомлення про помилку "відсутня збіжність". Ця помилка може бути викликана наступними причинами:
- Рівняння не має коренів.
- Коріння рівняння розташовані далеко від початкового наближення.
- Вираз має локальні максимуми або мінімуми між початковим наближенням і коренями.
- Вираз має розриви між початковим наближенням і коренями.
- Вираз має комплексний корінь, але початкове наближення було речовим (або навпаки).
Щоб встановити причину помилки, досліджуйте графік f (x). Він допоможе з'ясувати наявність коренів рівняння f (x) = 0 і, якщо вони є, то визначити приблизно їхні значення. Чим точніше вибрано початкове наближення кореня, тим швидше функція root буде сходитися до точного значення. roots; using plots to find
Деякі поради щодо використання функції root
У цьому розділі наведено кілька порад по використанню функції root:
- Для зміни точності, з яким функція root шукає корінь, можна змінити значення вбудованої змінної TOL. Якщо значення TOL збільшується, функція root буде сходитися швидше, але відповідь буде менш точний. Якщо значення TOL зменшується, функція root буде сходитися повільніше, але відповідь буде більш точний. Щоб змінити значення TOL в певній точці робочого документа, використовуйте визначення виду TOL: = 0.01. Щоб змінити значення TOL для усього робочого документа, виберіть з меню Математика команду Вбудовані змінні і введіть потрібне значення в поле TOL. Натиснувши "OK", виберіть з меню Математика команду Перерахувати все, щоб оновити всі обчислення в робочому документі з використанням нового значення змінної TOL.
- Якщо рівняння має кілька коренів, пробуйте використовувати різні початкові наближення, щоб знайти їх. Використання графіка функції корисно для знаходження числа коренів виразу, їх розташування і визначення відповідних початкових наближень. Малюнок 1 показує приклад. Якщо два кореня розташовані близько один від одного, можна зменшити TOL, щоб розрізнити їх.
- Якщо f (x) має малий нахил близько шуканого кореня, функція може сходитися до значення r, що відстоїть від кореня досить далеко. У таких випадках для знаходження більш точного значення кореня необхідно зменшити значення TOL. Інший варіант полягає в заміні рівняння f (x) = 0 на g (x) = 0, де
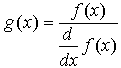
- Для вираження f (x) з відомим коренем a пошук додаткових коренів f (x) еквівалентний пошуку коренів рівняння h (x) = 0, де h (x) = f (x) / (x -a). Подібний прийом корисний для знаходження коренів, розташованих близько один до одного. Часто буває простіше шукати корінь виразу h (x), визначеного вище, ніж шукати інший корінь рівняння f (x) = 0, вибираючи різні початкові наближення.
Рішення рівнянь з параметром
Припустимо, що потрібно вирішувати рівняння багаторазово при зміні одного з параметрів цього рівняння. Наприклад, нехай потрібно вирішити рівняння для декількох різних значень параметра a. Найпростіший спосіб полягає у визначенні функції
f (a, x): = root (ex - a x 2, x)
Щоб вирішити рівняння для конкретного значення параметра a, надайте значення параметру a і початкове значення змінної x як аргументів цієї функції. Потім знайдіть шукане значення кореня, вводячи вираз f (a, x) =.
Малюнок 2 показує приклад того, як така функція може використовуватися для знаходження коренів досліджуваного рівняння при різних значеннях параметра. Зверніть увагу, що, хоча початкове значення x безпосередньо входить у визначення функції, немає необхідності визначати його в іншому місці робочого документа.
Малюнок 2: Визначення функції користувача з функцією root.
Знаходження коренів полінома
Для знаходження коренів виразу, що має вигляд
vnxn + ... + v2x2 + v1x + v0,
краще використовувати функцію polyroots, ніж root. На відміну від функції root, функція polyroots не вимагає початкового наближення. Крім того, функція polyroots повертає відразу всі корені, як речові, так і комплексні. На Малюнках 3 і 4 наведені приклади використання функції polyroots.
polyroots(V) Повертає корені полінома ступеня.Коефіцієнти полінома знаходяться у векторі v довжини n + 1.Повертає вектор довжини n, що складається з коренів полінома.
Функція polyroots завжди повертає значення коренів полінома, знайдені чисельно. Щоб знаходити коріння символьно, використовуйте команду Вирішити щодо змінної з меню Символіка. Див. Главу "Символьні обчислення" .
Малюнок 3: Використання функції polyroots для вирішення завдання, зображеної на рисунку 1.
Малюнок 4: Використання функції polyroots для пошуку коренів полінома.
Уважаемые зрители!
Коллектив Донецкого академического русского театра юного зрителя приглашает Вас каждую субботу в 15.00 на спектакли для взрослых зрителей, каждое воскресенье в 11.00 на музыкальные сказки для детей!
ВНИМАНИЕ! Лучшие спектакли нашего репертуара, доступные цены (15 - 20 грн. на представления для детей, 30-45 грн. – для взрослых), удобное время, комфорт и радушная театральная атмосфера!
Заказ билетов и справки по тел.: 6-46-01, 6-46-51
Касса работает ежедневно с 9:00 до 15:00
