Лекція № 2. Точка

1. Проекції точки на дві площини проекцій

Розглянемо проекції точок на дві площини, для чого візьмемо дві перпендикулярні площині (рис. 4), які будемо називати горизонтальній фронтальної і площинами. Лінію перетину даних площин називають віссю проекцій. На розглянуті площині спроеціруем одну точку А за допомогою плоскої проекції. Для цього необхідно опустити з даної точки перпендикуляри Аа і A на розглянуті площині.

Проекцію на горизонтальну площину називають горизонтальною проекцією точки А, а проекцію а? на фронтальну площину називають фронтальною проекцією.

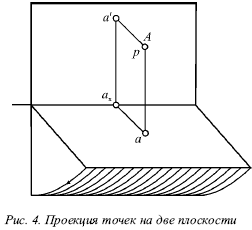
Точки, які підлягають проецированию, в нарисної геометрії прийнято позначати за допомогою великих латинських букв А, В, С. Для позначення горизонтальних проекцій точок застосовують малі літери а, b, с ... Фронтальні проекції позначають малими літерами з штрихом вгорі а ?, b ?, з? ...

Застосовується також і позначення точок римськими цифрами I, II, ... а для їх проекцій - арабськими цифрами 1, 2 ... �� 1 ?, 2? ...

При повороті горизонтальній площині на 90 ° можна отримати креслення, в якому обидві площині знаходяться в одній площині (рис. 5). Дана картина називається епюр точки.

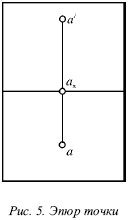
Через перпендикулярні прямі Аа і Аа? проведемо площину (рис. 4). Отримана площину є перпендикулярній фронтальній і горизонтальній площинах, тому що містить перпендикуляри до цих площинах. Отже, дана площину перпендикулярна лінії перетину площин. Отримана пряма перетинає горизонтальну площину по прямій аа х, а фронтальну площину - по прямій а? А х. Прямі аах і а? А х є перпендикулярними осі перетину площин. Тобто Ааах? є прямокутником.

При суміщенні горизонтальній і фронтальній площин проекції а й а? лежатимуть на одному перпендикуляр до осі перетину площин, так як при обертанні горизонтальній площині перпендикулярність відрізків аа х і а? а х не порушується.

Отримуємо, що на епюрі проекції а й а? деякої точки А завжди лежать на одному перпендикуляр до осі перетину площин.

Дві проекції а й а? деякої точки А можуть однозначно визначити її положення в просторі (рис. 4). Це підтверджується тим, що при побудові перпендикуляра з проекції а до горизонтальної площини він пройде через точку А. Точно так же перпендикуляр з проекції а? до фронтальної площини пройде через точку А, т. е. точка А знаходиться одночасно на двох конкретних прямих. Точка А є їхньою точкою перетину, т. Е. Є певною.

Розглянемо прямокутник Aaa х а? (Рис. 5), для якого справедливі наступні твердження:

1) Відстань точки А від фронтальної площини дорівнює відстані її горизонтальної проекції а від осі перетину площин, т. Е.

Аа? = Аа х;

2) відстань точки А від горизонтальної площини проекцій дорівнює відстані її фронтальної проекції а? від осі перетину площин, т. е.

Аа = а? А х.

Інакше кажучи, навіть без самої точки на епюрі, використовуючи тільки дві її проекції, можна дізнатися, на якій відстані від кожної з площин проекцій знаходиться дана точка.

Перетин двох площин проекцій розділяє простір на чотири частини, які називають чвертями (рис. 6).

Ось перетину площин ділить горизонтальну площину на дві чверті - передню і задню, а фронтальну площину - на верхню і нижню чверті. Верхню частину фронтальної площини і передню частину горизонтальній площині розглядають як межі першої чверті.

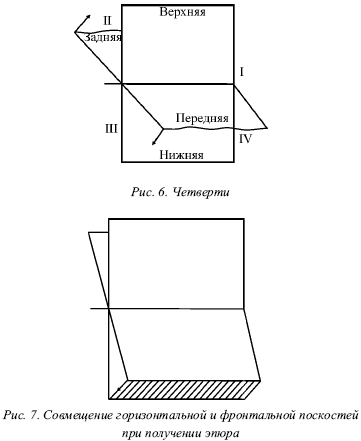
При отриманні епюра обертається горизонтальна площина і поєднується з фронтальним площиною (рис. 7). У цьому випадку передня частина горизонтальній площині співпаде з нижньою частиною фронтальної площини, а задня частина горизонтальній площині - з верхньою частиною фронтальної площини.

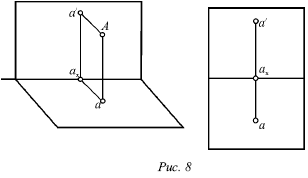
На малюнках 8-11 показані точки А, В, С, D, що розташовуються в різних чвертях простору. Точка А розташована в першій чверті, точка В - у другій, точка С - в третій і точка D - в четвертій.

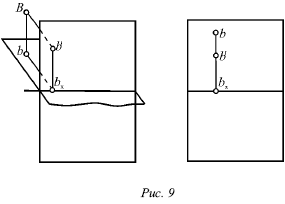
При розташуванні точок в першій або четвертій чвертях їх горизонтальні проекції знаходяться на передній частині горизонтальній площині, а на епюрі вони ляжуть нижче осі перетину площин. Коли точка розташована в другій або третій чверті, її горизонтальна проекція буде лежати на задній частині горизонтальній площині, а на епюрі буде знаходитися вище осі перетину площин.

Фронтальні проекції точок, які розташовані в першій або другій чвертях, будуть лежати на верхній частині фронтальній площині, а на епюрі будуть знаходитися вище осі перетину площин. Коли точка розташована в третій або четвертій чверті, її фронтальна проекція - нижче осі перетину площин.

Найчастіше при реальних побудовах фігуру розташовують в першій чверті простору.

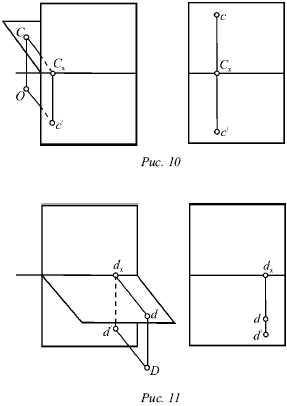
У деяких окремих випадках точка (Е) може лежати на горизонтальній площині (рис. 12). У цьому випадку її горизонтальна проекція е і сама точка будуть збігатися. Фронтальна проекція такої точки буде перебувати на осі перетину площин.

У разі, коли точка К лежить на фронтальній площині (рис. 13), її горизонтальна проекція k лежить на осі перетину площин, а фронтальна k? показує фактичне місцезнаходження цієї точки.

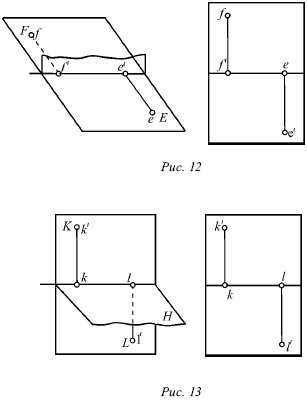
Для подібних точок ознакою того, що вона лежить на одній з площин проекцій, є те, що одна її проекція знаходиться на осі перетину площин.

Якщо точка лежить на осі перетину площин проекцій, вона і обидві її проекції збігаються.

Коли точка не лежить на площинах проекцій, вона називається точкою загального положення. Надалі, якщо немає особливих відміток, розглянута точка є точкою загального положення.

2. Відсутність осі проекцій

Для пояснення отримання на моделі проекцій точки на перпендикулярні площини проекцій (рис. 4) необхідно взяти шматок цупкого паперу у формі подовженого прямокутника. Його потрібно зігнути між проекціями. Лінія згину буде зображувати вісь перетину площин. Якщо після цього зігнутий шматок паперу знову розправити, отримаємо епюр, схожий на той, що зображений на малюнку.

Поєднуючи дві площини проекцій з площиною креслення, годі й показувати лінію згину, т. Е. Не проводити на епюрі вісь перетину площин.

При побудовах на епюрі завжди слід розташовувати проекції а й а? точки А на одній вертикальній прямій (рис. 14), яка перпендикулярна осі перетину площин. Тому, навіть якщо положення осі перетину площин залишається невизначеним, але її напрямок визначено, вісь перетину площин може перебувати на епюрі тільки перпендикулярно прямий аа? .

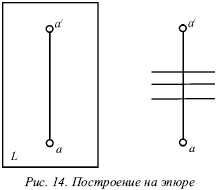
Якщо на епюрі точки немає осі проекцій, як на першому малюнку 14 а, можна уявити стан цієї точки в просторі. Для цього проведемо в будь-якому місці перпендикулярно прямий аа? вісь проекції, як на другому малюнку (рис. 14) і зігнемо креслення по цій осі. Якщо відновити перпендикуляри в точках а і а? до їх перетину, можна отримати точку А. При зміні положення осі проекцій виходять різні положення точки відносно площин проекцій, але невизначеність положення осі проекцій не впливає на взаємне розташування декількох точок або фігур в просторі.

3. Проекції точки на три площини проекцій

Розглянемо профільну площину проекцій. Проекції на дві перпендикулярні площині зазвичай визначають положення фігури і дають можливість дізнатися її справжні розміри і форму. Але бувають випадки, коли двох проекцій виявляється недостатньо. Тоді застосовують побудова третьої проекції.

Третю площину проекції проводять так, щоб вона була перпендикулярна одночасно обом площинам проекцій (рис. 15). Третю площину прийнято називати профільної.

У таких побудовах загальну пряму горизонтальній і фронтальній площин називають віссю х, загальну пряму горизонтальної та профільної площин - віссю у, а загальну пряму фронтальної і профільної площин - віссю z. Точка О, яка належить всім трьом площинам, називається точкою початку координат.

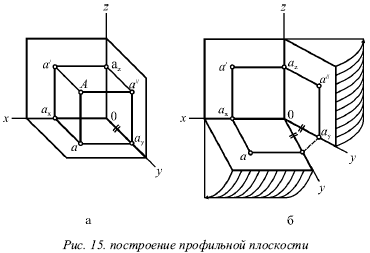
На малюнку 15а показана точка А і три її проекції. Проекцію на профільну площину (а ??) називають профільної проекцією і позначають а ?? .

Для отримання епюра точки А, яка складається з трьох проекцій а, а а, необхідно розрізати тригранник, що утворюється усіма площинами, уздовж осі у (рис. 15б) і поєднати всі ці площини з площиною фронтальній проекції. Горизонтальну площину необхідно обертати близько осі х, а профільну площину - близько осі z в напрямі, вказаному на малюнку 15 стрілкою.

На малюнку 16 зображено положення проекцій а, га? і а ?? точки А, отримане в результаті поєднання всіх трьох площин з площиною креслення.

В результаті розтину вісь у зустрічається на епюрі в двох різних місцях. На горизонтальній площині (рис. 16) вона приймає вертикальне положення (перпендикулярно осі х), а на профільній площині - горизонтальне (перпендикулярно осі z).

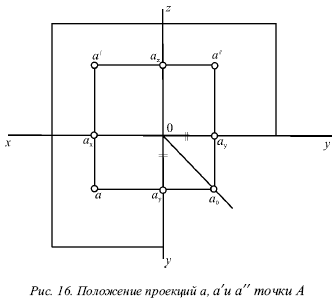
На малюнку 16 три проекції а, га? і а ?? точки А мають на епюрі строго певне положення і підпорядковані однозначним умов:

1) горизонтальна і фронтальна проекції а й а? завжди повинні розташовуватися на одній вертикальній прямій, перпендикулярній осі х;

2) фронтальна і профільна проекції а? і а ?? завжди повинні розташовуватися на одній горизонтальній прямій, перпендикулярній осі z;

3) при проведенні через горизонтальну проекцію а горизонтальної прямої, а через профільну проекцію а ?? - вертикальної прямої побудовані прямі обов'язково перетнуться на бісектрисі кута між осями проекцій, тому що фігура Оа у а 0 а н - квадрат.

При виконанні побудови трьох проекцій точки потрібно перевіряти виконуваність всіх трьох умов для кожної точки.

4. Координати точки

Положення точки в просторі може бути визначено за допомогою трьох чисел, які називаються її координатами. Кожній координаті відповідає відстань точки від якої-небудь площини проекцій.

Відстань обумовленої точки А до профільної площини є координатою х, при цьому х = а? А (рис. 15), відстань до фронтальної площини - координатою у, причому у = а? А, а відстань до горизонтальної площини - координатою z, при цьому z = aA.

На малюнку 15 точка А займає ширину прямокутного паралелепіпеда, і вимірювання цього паралелепіпеда відповідають координатам цієї точки, т. Е., Кожна з координат представлена ​​на малюнку 15 чотири рази, т. Е .:

х = а? А = ОАХ = Ауа = aza ?;

y = а? А = Оаy = аxа = аzа ?;

z = aA = Oaz = аxа? = Аyа ?.

На епюрі (рис. 16) координати х і z зустрічаються по три рази:

х = аzа? = Оаx = аyа,

z = аxa? = Oaz = аyа ?.

Всі відрізки, які відповідають координаті х (або z), є паралельними між собою. Координата у два рази представлена віссю, розташованою вертикально:

y = ТАУ = аха

і два рази - розташованої горизонтально:

у = ТАУ = аzа ?.

Дана відмінність з'явилося через те, що вісь у присутній на епюрі в двох різних положеннях.

Слід врахувати, що положення кожної проекції визначається на епюрі тільки двома координатами, а саме:

1) горизонтальної - координатами х і у,

2) фронтальної - координатами x і z,

3) профільної - координатами у і z.

Використовуючи координати х, у і z, можна побудувати проекції точки на епюрі.

Якщо точка А задається координатами, їх запис визначається так: А (х; у; z).

При побудові проекцій точки А потрібно перевіряти виконуваність наступних умов:

1) горизонтальна і фронтальна проекції а й а? повинні розташовуватися на одному перпендикуляр до осі х, так як мають загальну координату х;

2) фронтальна і профільна проекції а? і а? повинні розташовуватися на одному перпендикуляр до осі z, так як мають загальну координату z;

3) горизонтальна проекція а так само віддалена від осі х, як і профільна проекція а віддалена від осі z, так як проекції а? і а? мають загальну координату у.

У разі, якщо точка лежить в будь-який з площин проекцій, то одна з її координат дорівнює нулю.

Коли точка лежить на осі проекцій, дві її координати дорівнюють нулю.

Якщо точка лежить на початку координат, все три її координати дорівнюють нулю.