- Ко Дню Святого Валентина
- ТЮЗ остается в Макеевке
- С Новым годом
- Гуманитарная помощь
- Театральные встречи
- Открылся 44 театральный сезон!!!
- Для льготников!
- Положення про фестиваль
- ТЮЗ - 2007
- ТЮЗ - 2009
- Сведения об участниках фестиваля ТЮЗ-2009
- ТЮЗ-2011
- ПРОГРАМА Третього відкритого фестивалю театрів для дітей та юнацтва «ТЮГ-2011»
- Итоги Третьего открытого фестиваля театров для детей и юношества ТЮЗ-2011
- Пресс-релиз IV Открытого фестиваля театров для детей июношества «ТЮЗ – 2013».
- Итоги IV открытого фестиваля театров для детей и юношества «ТЮЗ – 2013»
Наш бизнес-сообщник artMisto.net
Нарисна геометрія
Накреслити а кові геом е трия, розділ геометрії, в якому просторові фігури вивчаються за допомогою побудови їх зображень на площині, зокрема побудови проекційних зображень, а також методи вирішення і дослідження просторових задач на площині.
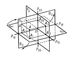
Потреба в зображеннях просторових предметів на площині виникла в зв'язку з рішенням різних практичних питань (наприклад, будівництво будівель і інших інженерних споруд, розвиток живопису і архітектури, техніки і т.п.). Особливо велике значення мають креслення, одержувані проектуванням (проектуванням) даної фігури на площину (проекційні креслення). Практика пред'являла до таких кресленнями ряд вимог; найважливіші з них: 1) наочність зображення, т. е. властивість креслення викликати просторове уявлення зображуваної фігури; 2) «оборотність» креслення, т. Е. Можливість точного визначення змальованої фігури по кресленням; 3) простота виконання необхідних побудов; 4) точність графічних рішень. У способах побудови зображень застосовуються центральне і паралельне проектування фігури (натури, об'єкту, оригіналу) на площину проекцій (див. проекція ). Найбільшою наочністю володіють креслення, отримані способом центрального проектування, який відповідає геометричній схемі виникнення зображень на сітківці ока. Однак найбільш вживаними в Н. р є паралельні проекції, які простіші в побудові зображень і зручніші для визначення по ним натуральної фігури. Існують різні види паралельних проекцій; найпоширенішим є спосіб ортогональної проекції на дві або три площини (комплексне креслення). Суть цього способу полягає в наступному. Вибирають дві взаємно перпендикулярні площини проекцій П1 і П2 в просторі. Площина П1 розташовують горизонтально; її називають горизонтально і площиною проекцій, а площину П2 - фронтальної площиною проекцій. Довільну точку А простору проектують ортогонально на ці площини (рис. 1); отримують горизонтальну проекцію A1 (AA1 (площині П1) і фронтальну проекцію A2 (AA2 ^ площині П2). Три точки А, A1 і A2 лежать в одній (що проектує) площині, перпендикулярній до лінії p12 перетину площин проекцій. Горизонтальну проекцію будь-якої фігури отримують, проектуючи ортогонально всі точки цієї фігури на площину П1, фронтальну проекцію - на площину П2. Часто буває корисно додати третю проекцію фігури - на площину П3, перпендикулярну до площин П1 і П2. площина П3, а також і проекцію на неї називають профільною. дві проекції точки А (наприклад, A1 і A2) цілком визначають третю проекцію (A3).
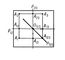
Щоб отримати креслення, що складається з трьох зазначених проекцій (комплексне креслення), площини П1 і П3 поєднують з площиною П2 ( «головною» площиною) шляхом обертання їх навколо ліній p12 і p23 перетину цих площин з площиною П2 (рис. 2). Зазвичай на практиці не вказується положення осей проекцій p12 і p13, тобто положення площин проекцій визначається з точністю до паралельного переносу.
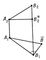
Комплексне креслення звернемо, тому що по ньому можна визначити відстань між будь-якими двома точками натуральної фігури. Дійсно, відрізок AB (рис. 3) в натурі є гіпотенузою прямокутного трикутника ABB *, в якому AB * = A1B1, а В * В є різниця висот точок В і А, що виражається на кресленні відрізком B2 * B2. Звідси можна отримати просту побудову натурального відрізка
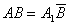
(Рис. 4); для цього потрібно побудувати
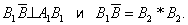
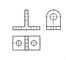
Для збільшення наочності комплексного креслення на проекціях фігури встановлюють «умови видимості»: з двох точок А і В, проекції яких на будь-якої з площин проекцій збігаються, наприклад A1 º B1, видимої вважається та, яка розташована ближче до глядача; «Невидимі» лінії фігури умовно зображаються штриховими лініями. Приклад такого зображення просторової фігури в трьох проекціях, називається «вид спереду» (фронтальна проекція), «вид зверху» (горизонтальна проекція) і «вид зліва» (профільна проекція), дан на мал. 5.
Комплексне креслення (з двох або трьох ортогональних проекцій) є найбільш поширеним видом технічного креслення. По ньому легко визначаються всі необхідні розміри зображуваного предмета. Недолік таких креслень - їх мала наочність.
Для побудови більш наочних оборотних зображень в Н. р застосовується інший спосіб, званий аксонометрією.
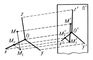
При аксонометрии зображає фігуру відносять до системи Oxyz осей координат в просторі (див. аналітична геометрія ). Цю систему координат називають натуральною. На рис.6 побудована координатна ламана OMxM1M для довільної точки М. Довжини координатних відрізків OMx, MxM1, M1M є координатами х, у, z точки М. Якщо спроектувати натуральну систему осей Охуz на площину П ', то виходить так звана аксонометрична система осей Про 'х'у'z' (рис. 6). Проекція O'M'xM'1M 'координатною ламаною складається з відрізків O'M'x, M'xM'1, M'1M', довжини яких x ', y', z 'в аксонометрической системі координат називається аксонометричними координатами точки М . Відносини
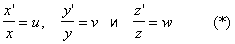
висловлюють величини спотворення координатних відрізків при проектуванні; їх називають показниками (коефіцієнтами) спотворення. Якщо всі три показники спотворення рівні, то аксонометрію називають ізометрією, якщо хоча б два з них рівні - діаметром, якщо ж всі показники спотворення нерівні - триметр.
Щоб за допомогою аксонометричного способу побудувати зображення точки М на площині П 'в даній паралельній проекції, необхідно мати: а) натуральні координати цієї точки М (х, у, z); б) аксонометрическую систему осей О''х''у''z '' на площині проекцій П '; в) показники спотворення u, v, w.
Тоді за формулами (*) знаходять аксонометричні координати точки М '(х', у ', z') і будують по ним точку M ', яка є шуканої проекцією точки М. Аксонометричне зображення просторової фігури будують по крапках, що визначають останню. Аксонометричний креслення звернемо: якщо на аксонометричному кресленні дана точка M '(х', у ', z'), то можна по формулах (*) знайти натуральні координати х, у, z точки М.
Якщо задати довільну аксонометрическую систему осей O'x'y'z 'на площині проекцій П' (що не зводиться, однак, до однієї прямої) і відношення показників спотворення u: v: w, то, згідно з основною теоремою аксонометрии ( польці теоремі ), Існує таке положення натуральної системи осей координат відносно площини проекцій П 'і такий напрям проектування, при яких на площині П' реалізуються раніше вибрана аксонометрична система осей і відносин показників спотворення.
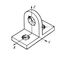
Для спрощення аксонометричного способу побудови зображень користуються «приведеною» аксонометрією, в якій аксонометричні координати прагнуть по можливості замінити натуральними без спотворення вигляду креслення. Так, наприклад, на рис. 7 дана ортогональна ізометрія об'єкту, зображеного на комплексному кресленні (рис. 5), з використанням натуральних координат замість аксонометричних. При цьому відбувається зміна масштабу аксонометричного креслення, але вигляд його зберігається, т. Е. Креслення змінюється подібно. Аксонометріческіе зображення предметів, що не мають великої протяжності, володіють достатньою наочністю. Цього не можна сказати про зображення крупних об'єктів, таких, як будівлі, греблі та ін. Споруди. У цих випадках краще застосовувати зображення, виконані в центральній проекції ( перспективі ).
Щоб перспективний креслення було оборотним, на площині проекцій П 'будують центральну проекцію A' (перспективу) зображуваної точки А і перспективу A1 'ортогональної проекції A1 точки на горизонтальну площину П1, звану предметної (рис. 8). Площина проекцій П '(картинну площину) вибирають переважно перпендикулярної до предметної. Точка A1 називається підставою точки А. Зокрема, S1 є підстава центру проекцій ( «очі») S. Знаючи положення центру S відносно картинної площини П ', можна за даними перспективі A' точки А і перспективі A'1 її заснування визначити місце розташування натуральної точки А в просторі. Для цього потрібно провести SA1 'і знайти A1. Потім побудувати A1A ^ площині П1 і знайти точку А перетину прямих SA 'і A1A. Велике значення при побудові перспективних зображень мають т. Н. точки сходу, які є перспективними зображеннями нескінченно видалених точок простору, і лінія горизонту - перспективне зображення нескінченно видаленої прямої предметної площині П1.
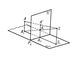
На рис. 9 показано перспективне зображення кімнати. На ньому видно головна точка y '¥, яка є точкою сходу для всіх прямих, перпендикулярних (у натурі) картинній площині, і лінія горизонту h. Точки сходу ін. Паралельних прямих, що лежать в предметній площині, розташовуються на лінії горизонту h (наприклад, D '¥).
Використовуючи координатний метод, можна виконати побудову перспективного зображення за способом центральної аксонометрии, аналогічно описаної вище паралельної аксонометрии.
Поряд з побудовами перспективних зображень на площині (лінійна перспектива) на практиці вживаються і ін. Види центрально-проекційних зображень.
При побудові креслень, що зображують будь-яку частину земної поверхні, зручно користуватися так званими проекціями з числовими відмітками. У цьому випадку на кресленні має бути задане достатнє число точок поверхні (рис. 10). Проектуючи ортогонально точки поверхні на площину проекцій, записують близько проекції кожної точки її висотну позначку, т. Е. Число, що виражає висоту точки над площиною проекцій в вибраних одиницях довжини. Завдяки цьому такий креслення є оборотним. Для збільшення його наочності та зручності користування, проекції точок, що мають однакову висоту, з'єднують лінією, яку називають лінією рівня. Якщо зображена земна поверхня, то площину проекцій вважається горизонтальною; лінії рівня називають в цьому випадку горизонталями. За формою і розташуванню горизонталей можна (з певним ступенем точності) судити про рельєф зображеного ділянки земної поверхні, побудувати її перетин заданою на кресленні площиною s (рис. 10), а також вирішувати інші завдання. Такий спосіб зображення поверхні і саму поверхню, задану системою горизонталей, називають топографічними.
Історична довідка. Перші спроби проекційних зображень можна зустріти у древніх народів ще до нашої ери. Так, римський архітектор Вітрувій в своєму творі «Десять книг про архітектуру» (1 ст. До н. Е.) Дає поняття про план (горизонтальній проекції) і фасаді (фронтальній проекції) споруди. Італійський архітектор і вчений Л. Альберти (15 в. Н. Е.) Вже застосовує «точки сходу» і дає важливий для практики спосіб побудови перспективи за допомогою сітки. У «Трактаті про живопис» (опублікований тисячі шістсот п'ятьдесят один) Леонардо да Вінчі є численні вказівки про практичних цілях перспективних зображень, зокрема про «спостережної» перспективі. Німецький художник А. Дюрер в праці «Керівництво до виміру ...» (1 525) запропонував спосіб побудови перспективи по горизонтальній і фронтальній проекціях об'єкту. Особливо повний виклад прийомів побудови перспективи були дані італійським вченим Г. Убальди (1600). Наукові основи Н. р були розроблені Ж. Дезаргом і головним чином Г. Монжем , Який вважається творцем наукової Н. р
У Древній Русі при зведенні споруд застосовувалися зображення, в яких можна помітити елементи геометричного проектування. Так, зображення міста Пскова (1581) було виконано з дотриманням деяких законів перспективи. Креслення винахідника-самоучки І. П. Кулібіна , Зодчого Д. В. Ухтомського і ін. є геометрично правильними проекційними зображеннями. Курс Н. р був вперше введений в 1810 в Петербурзькому інституті корпусу інженерів шляхів сполучення. Першим російським професором Н. р був Я. А. Севастьянов, який написав ряд творів з різних питань Н. р Науковому розвитку Н. р сприяли геометричні роботи Е. С. Федорова , Який запропонував метод зображення точок простору на площині за допомогою векторів. Метод Е. С. Федорова був успішно застосований в багатовимірної Н. р, яка використовується в фізико-хімічному аналізі (школа Н. С. Курнакова). Радянські геометри (А. К. Власов, Н. А. Глаголєв, Н. Ф. Четверухин і ін.) Виконали ряд досліджень в області основної теореми аксонометрии.
Літ .: Ринін Н. А., Матеріали до історії нарисної геометрії, [Бібліографія, біографії, епізоди, факти, хронологія], Л., 1938; Монж Г., Нарисна геометрія, пров. з [франц.], М., 1947; Федоров Е. С., Нова нарисна геометрія, «Изв. АН », 1917, № 10; Глаголєв Н. А., Нарисна геометрія, 3 вид., М., 1953; Вольберг О. А., Лекції з нарисної геометрії, М. - Л., 1947; Курс нарисної геометрії, під ред. Н. Ф. Четверухина, М., 1956; Питання сучасної нарисної геометрії. Зб. ст., під ред. Н. Ф. Четверухина, М. - Л., 1947; Глазунов Є. А. і Четверухин Н. Ф., Аксонометрія, М., 1953: Методи нарисної геометрії і її додатки. Зб. ст., під ред. Н. Ф. Четверухина, М., 1955; Добряков А. І., Курс нарисної геометрії, 3 вид., М. - Л., 1952.
Н. Ф. Четверухин.

Мал. 10 до ст. Нарисна геометрія.
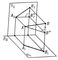
Мал. 3 до ст. Нарисна геометрія.
Мал. 6 до ст. Нарисна геометрія.

Мал. 9 до ст. Нарисна геометрія.
Мал. 8 до ст. Нарисна геометрія.
Мал. 7 до ст. Нарисна геометрія.
Мал. 4 до ст. Нарисна геометрія.
Мал. 2 до ст. Нарисна геометрія.
Мал. 5 до ст. Нарисна геометрія.
Мал. 1 до ст. Нарисна геометрія.
Уважаемые зрители!
Коллектив Донецкого академического русского театра юного зрителя приглашает Вас каждую субботу в 15.00 на спектакли для взрослых зрителей, каждое воскресенье в 11.00 на музыкальные сказки для детей!
ВНИМАНИЕ! Лучшие спектакли нашего репертуара, доступные цены (15 - 20 грн. на представления для детей, 30-45 грн. – для взрослых), удобное время, комфорт и радушная театральная атмосфера!
Заказ билетов и справки по тел.: 6-46-01, 6-46-51
Касса работает ежедневно с 9:00 до 15:00
